Efficiency

The efficiency of a trebuchet is a measure of how well the trebuchet performed compared to an ideal trebuchet. VirtualTrebuchet has two types of efficiency, Energy Efficiency, and Range Efficiency.

In the case of finding Energy Efficiency, an ideal trebuchet is one that converts all its potential energy before the launch onto kinetic energy and potential energy in the projectile at release. The expression for Energy Efficiency, ηenergy, is,

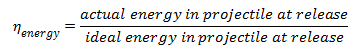
Since the ideal trebuchet gives all its energy to the projectile, the efficiency can be rewritten as,

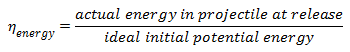
A trebuchet with good Energy Efficiency does not necessarily shoot very far because the equation for Energy Efficiency ignores direction the projectile is launched. The projectile could be launched straight up so that it lands right back on the trebuchet, and the trebuchet may still have a good Energy Efficiency. This is why there is also Range Efficiency. For Range Efficiency, the ideal trebuchet is one that gives all its initial potential energy to the projectile, and launches it at 45° from horizontal. 45° is not usually the ideal release angle for a trebuchet, but that is because the projectile usually gains some extra velocity by staying in the sling longer. However, for a given launch velocity, 45° is the optimal angle to use to get the projectile to shoot the farthest possible. The ideal trebuchet ignores air resistance. The expression for Range Efficiency, ηrange, is,

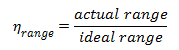
Errors

This is a list of the errors messages that may be encountered.

The simulation timed out in Stage 1.

If the trebuchet does not transition out of stage 1 in 10 seconds, the simulation will end without going on to stage 2.

The simulation timed out in Stage 2.

If the trebuchet does not transition out of stage 3 in 20 seconds, the simulation will end without going on to stage 3.

The simulation timed out in Stage 3.

If the projectile does not land within 3 minutes, the simulation will end.

The trebuchet arm went through the ground.

The counterweight went through the ground.

The sling was not in tension for the whole launch.

In the simulation, the sling is modeled as a rigid component that has a constant length even if it is in compression. In reality the sling only works in tension. This error message tells you that the sling was in compression for some period of time, so the results probably do not reflect reality. The sling also turns red while it is in compression.

The integration step size went to the minimum allowed value, so the simulation results may be questionable.

The simulation uses numerical integration to solve the trebuchet equations. Normally the simulation adjusts the step size used in the numerical integration to get accurate results, but there is a minimum step size. This error message says the step size would need to go below that minimum to get good results. For more information see the Example Problem, and Runge-Kutta section.

The check function went to XX.XXX, which is larger than expected, so the simulation results may be questionable.

There is a check function that is in the simulation to make sure the trebuchet is behaving properly. If the trebuchet is behaving well, the check function stays very close to zero. If the check function goes above 0.00001, the simulation will show this error message.

A negative value was entered for one or more of the length parameters. Expect odd behavior in the results.

The simulator will give results if the length parameters have negative values, however odd behavior has been observed in the transitions between stages in some cases. Not much effort has gone into debugging odd behavior that the negative values may produce.