Uniform Arm
When Uniform Arm is selected the program makes the assumption that the arm has a uniform cross-section along its whole length. If the arm has a uniform cross-section then its center of gravity is exactly in the center of the arm and the program can automatically calculate the value for Pivot to Arm CG. The value Inertia of Arm can also be automatically calculated if the arm has a constant cross-sections.
While the Uniform Arm option is convenient, most real trebuchets usually have a tapered arm which tends to have better performance.
Mass of Arm
Mass of Arm is the mass of the entire arm, which includes the parts defined by Length of Short Arm and Length of Long Arm.
For the best performance, the arm should be as light as possible.
Inertia of Arm
Inertia of Arm is the moment of inertia of the entire arm around its center of gravity.
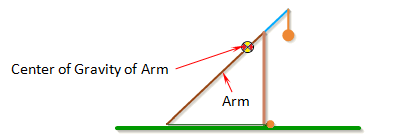
For an arm with a uniform cross-section along its length, the moment of inertia can be approximated by the formula,
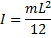
where m is the mass of the arm, and L is the total length of the arm (Length of Long Arm + Length of Short Arm).
For a non-uniform arm, the moment of inertia can be found by breaking the arm up into simple shapes, finding the moment of inertia for each one, and then combining them together using the parallel axis theorem. A list of formulas for the moment of inertia of different shapes can be found here. See the Arm Example Calculations.
Alternatly, using a 3D CAD software package is probably the easiest way to find the inertia of a non-uniform arm.
For best performance, the moment of inertia of the arm should be as small as possible. This is why the arm is tapered on many trebuchets.
Note: When Auto Calculate is checked, the arm is assumed to have a uniform cross-section and the Inertia of Arm will be calculated automatically.
Pivot to Arm CG
Pivot to Arm CG is the distance between the pivot point and the center of gravity of the arm.
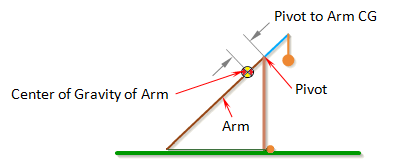
The center of gravity of the arm is the average location of the gravitational force acting on the arm. If the arm has a uniform cross-section along its length, then its center of gravity will be located exactly at the center the arm.
For a non-uniform arm, the center of gravity can be found by breaking the arm up into simple shapes, finding the center of mass of each one, and taking the mass-weighted average of the different parts. See the Arm Example Calculations.
Alternately, the center of gravity can be found by hanging the arm horizontally from a string, and moving the string along the arm until it balances. It will balance when the string is at the center of gravity.
For the best performance, the center of gravity of the arm should be as close to the end of the arm that the weight is attached to as possible.
Note: When Auto Calculate is checked, the arm is assumed to have a uniform cross-section and the Pivot to Arm CG will be calculated automatically.