Arm Example Calculations
This is an example of how to calculate the center of gravity and inertia for a non-uniform arm.
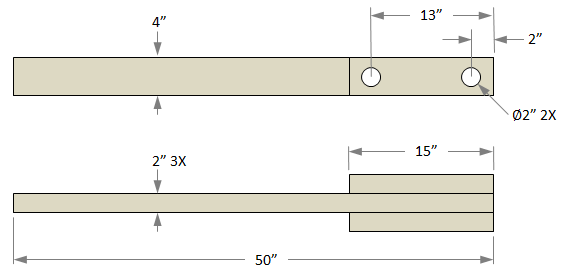
This arm is made of white pine which has a density of 0.015 lb/in³. We will first split the arm into its different components to find the mass for each one.
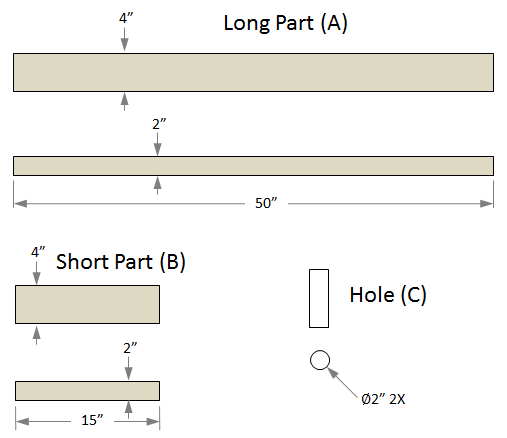
In order to make the calculations easier we will make Part A and Part B solid, and treat the holes as a separate part with negative mass.
mass A = (Volume A) x (Density A) = (50 in) x (4 in) x (2 in) x (0.015 lb/in³) = 6 lb
mass B = (Volume B) x (Density B) = (15 in) x (4 in) x (2 in) x (0.015 lb/in³) = 1.8 lb
mass C = (Volume C) x (Density C) = π x ((2 in)/2)² x (6 in) x (-0.015 lb/in³) = -0.283 lb
Total Mass of Arm = (Mass A) + 2 x (Mass B) + 2 x (Mass C) = 9.034 lb
We will find the center of gravity of the arm by taking the mass average of the center of gravity locations of each component.
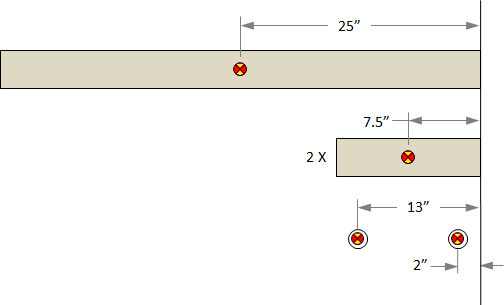
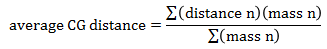
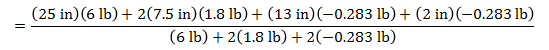
average CG distance = 19.1 in
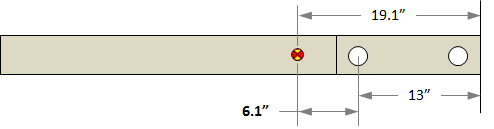
What we really want is the Pivot To Arm CG distance. We can get this by subtracting the average CG distance of by the distance from the pivot hole to the end of the arm.
Pivot To Arm CG = 19.1 in - 13 in = 6.1 in
Now that we have the location of the center of gravity of the arm, we can calculate the inertia of the arm. First we need to calculate the inertia of each component. The inertia for a cuboid is given by,
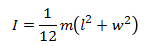
The inertia for a cylinder about its axis is given by,
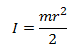
The inertias for the different components are,
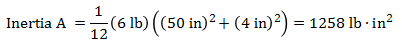
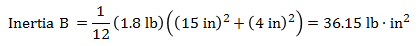
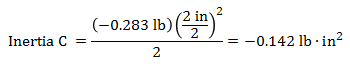
Now that we have the inertias of the individual components, we can use the parallel axis theorem to find the inertia of the whole arm. The parallel axis theorem is,
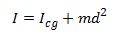
where Icg is the inertia of a body about its center of gravity, m is the mass of the
body, and d is the distance between the center of gravity of the body and the axis about which you
want to calculate the inertia (in this case the center of gravity of the whole arm). The following
picture shows the d values for the different bodies.
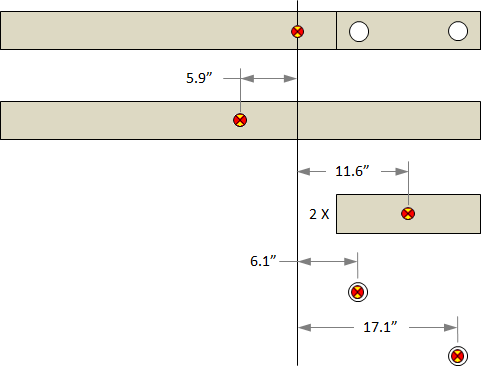
Now we can find the inertia of the arm.
Inertia A about arm CG = (1258 lb∙in²) + (6 lb) x (5.9 in)² = 1466.9 lb∙in²
Inertia B about arm CG = (36.15 lb∙in²) + (1.8 lb) x (11.6 in)² = 278.4 lb∙in²
Inertia C1 about arm CG = (-0.142 lb∙in²) + (-0.283 lb) x (6.1 in)² = -10.7 lb∙in²
Inertia C2 about arm CG = (-0.142 lb∙in²) + (-0.283 lb) x (17.1 in)² = -82.9 lb∙in²
Inertia of Arm = (1466.9 lb∙in²) + 2 x (278.4 lb∙in²) + (-10.7 lb∙in²) + (-82.9 lb∙in²) = 1930 lb∙in²